Article / 评论文章
温州航海学院,浙江,温州,中国
梁世铎
温州航海学院,浙江,温州,中国
2022 年 4 月 28 日 ; 2022 年 5 月 12 日
天体事件时间间隔测下的为t,t只是地球时,不为天体事件原时t。,必须把地球时t转换成天体事件原时t。。
测下天体视向速度u,不是天体本征速度,本征速度是不变的,而视速率是变化的,向着太阳系靠近运动的天体是兰移天体,兰移天体的视速率,一年比一年慢。
巴纳德星是兰移天体,是一例证,视速率年年在变慢,第一次测下的视速率为110.8km/s,(ARICNS:1916年),第二次测下的视速率为106.8km/s(SIMBAD:2000年)。由此本文计算出:巴纳德星的本征速度为959.332km/s,2022年视速率为105.751km/s。
视分量角、视速率、兰、红移临界点、巴纳德星 中图分类号:F.P129 文献标识码:A
视分量角:天体运动方向线与天体至测者视线的夹角,见图1
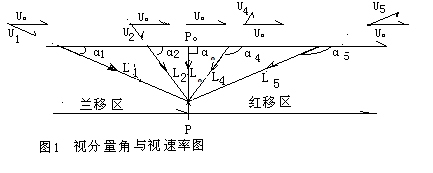
由图中知,天体由靠近太阳系运动(兰.移)至背离太阳系运动(红移)过程,视分量角都在渐渐变大,α1<α2<α。<α4<α5。
视速率:运动天体至测者视线向的速度,兰移天体视速率在渐渐变慢,至临界点P。,视速率为0。过了临界点,由兰移变为红移,视速率渐渐在变快。宇宙间运动源这一运动性质是共性的,这也包括雷达测速仪对汽车的测速。
作者用欧伦福平板PSD-3型雷达测速仪(K波:f。=2.413209697× 1010 Hz),在直道公路上,对准行驶的小车(36km/h),如图1的实验,数据如图2【1】
小车驶近测者(兰移区)时,视速率(为+号)渐渐变小,到达P。(正横)时,视速率为零, 过P。点,驶离测者(红移区)时,视速率(为-号)渐渐变大,P。为兰、红移临界点。
观测初始频率f1<=f。+1609Hz,至P。点时,观测频率f3=f。+0,末了观测频率f5=f。-1609Hz, 观测频率由高渐渐至低;f1>f3>f5 ,观测周期都在渐渐变慢【2】,因视分量角都在渐渐变大。
上述状态,是普适的观测规律,也能适应普遍的运动天体。为了能得到天文学上实测例证,必须找一个年自行值很大的天体,来论证这一论说。
多数的天体,年自行值,不超过1角秒,而巴纳德星有很大的年自行值。巴纳德星【3】靠近太阳系运动(兰移星),是美国天文学家巴纳德(Edward Emeron Barnard,1875-1923)在1916年发现的。
年自行值10.3角秒,ARICNS视速率(U1)为110.8km/s(1916年),而SIMBAD年自行值10.31角秒,视速率(U2)为106.8km/s(2000年)。见图3
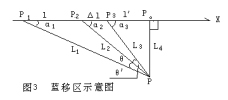
设巴纳德星本征速度为U。,
视速率U1=U。cosα1, 视速率U2=U。cosα2,
U。=U1/cosα1=U2/cosα2=U2/cos(α1+θ)=U2/(cosα1 cosθ-sinα1sinθ)
整理:U2/U1=(cosα1cosθ-sinα1sinθ)/cosα1,=cosθ-tgα1 sinθ
得:求视分量角式:
tg α1=(cosθ-U2/U1)/sinθ [1]
1916年至2000年,计 84年,巴纳德星共自行了θ=[(10″.3+10″.31)÷2×84]
θ=0°14′25.62″
将θ=0°14′25.62″ U1=110.8km/s U2=106.8km/s 代入[1]式
得:tg α1=8.600296206 α1 =83°22′3.76″ α2=83°36′29.38″
巴纳德星运动本征速度U。 =U1/cosα1 =959.3328316km/s U。=U2/cosα2=959.3328316km/s
2000年至2022年,计t′=22年,巴纳德星自行了θ′=10.31″×22=0°3′46.82″,
巴纳德星2022年视分量角α3=α2+θ′=83°40′16.2″,
巴纳德星2022年视速率为U3=cosα3U。=105.751km/s !
将地球时(t)转换成巴纳德星时(t。),
视分量角为α2时:
t。2 =t′/(1-Cosα2 U。/C。) [2]
将:t′=22年 α2 =83°36′29.38″ U。=959.3328316km/s C。=299792.458km/s
代入[2]式 得:t。2 =22.00784022年
将:t′=22年 a3=83°40′16.2″ U。 C。代入[2]式
得:t。3 =22.00776322年
t。=(t。2 +t。3)/2=22.00780172年
巴纳德星在t。(22.00780172年)时间内运动了Δl路程,
Δl=t。U。/C。=0.07042474278光年
L3=Δl Sinα2/Sinθ′ [3]
将:Δl=0.07042474278光年 α2=83°36′29.38″ θ′=0°3′46.82″代入[3]式
得:L3=63.64452522光年 t3 =63.64452522年 。
L2=Δl Sinα3/Sinθ′ [4]
将:α3=83°40′16.2″、Δl 、θ′等代入[4]式
得:L2=63.65232694光年 t2=63.65232694年 。
验证;两艘飞船②、③,同时从X轴P2点出发,飞船②以光速向P点飞行,经过t2时间到达P点,在P点等候,飞船③沿X轴以U。速率飞行,经过t。时间到达P3点,瞬而以光速向P点飞行,经过t3时间到达P点,此瞬间飞船②已等候了t时间间隔。飞船②与飞船③计时时长相等,只不过飞船②在P点早到了t时间隔,
故:t2 + t = t。+ t3 = T [5]
将以上数据代入[5]式:得 63.65232694年+22年=22.00780172年+63.64452522年
t2 + t = 85.65232694年=T
t3 + t。= 85.65232694年=T 见图3-1
l′ =L3cosα3 [6]
将:L3=63.64452522光年 α3=83°40′16.2″代入[6]式,得:l′=7.0158光年
将巴纳德星时2192.4年(t″。=l′C。/U。)转换成地球时(t″)
t″。+t4=t″+t3 [7]
将t″。=2192.4年 t4=63.25560958年 t3=63.64452522年代入[7]式
得:t″=2192年,
巴纳德星将于公元4214最接近太阳系,到达地球天顶(P。),界时巴纳德星:视分量角π/2,视速率为0 。
由4式:L2=Δl Sinα3/Sinθ′
L2 = ΔlSiin(a2+θ′)/ Sinθ′=Δl(Sina2 Cosθ′+Cosa2 Sinθ′)/Sinθ′
L2/Δl=Sina2/tgθ′+Cosa2
整理得:tgθ′=Sina2/( L2/Δl – Cosa2 ) [8]
[8]式;天体自行式,变为普适式
tgθ = Sinan /(Ln/Δl n -Cosan ) [8]
光源以U。速度沿S系X轴运动,发生了多普勒效应,如图3-2 A,此时有五位静止的测者,在五个位子上对光源进行测速,①测者在光源运动方向上,视分量角为0度,②测者视分量角为α2 ,③测者视分量角为α3(90度),④侧者视分量角为α4 ,⑤测者视分量角为α5(180度)。
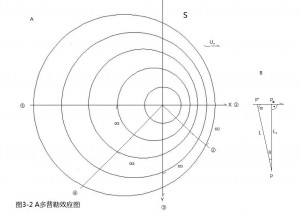
对于①测者,光源是兰移的,视速为本征速度U。。对于②测者,光源是兰移的,视速为
U2(U2=U。Cosα2)。对于④测者,光源是红移的,视速为U4(U4=U。Cosα4)。对于⑤测者,光源是红移的,视速为本征速度U。。
对于③测者,视速为0,如同光源相对测者静止了,因光波从光源到达测者的光程都同等,测者测下视速为0,见图3-2 B;光源运动到接近P。的P’点时,与测者相距L光程,视分量角为α(α=α3 -θ 或α=α3+θ),光程L=L。/sinα=L。/sin(α3±θ)
L = L。/cosθ [9]
由[9]式知道,θ角渐小到于2角秒时(cosθ=1),L=L。,光波由光源到达测者的光程,同等于L。,此时测下的光源等同相对测者静止。[9]式等同于光源相对测者静止时,光波以同等的光程到达测者来描述的,而视速率U=U。Cosα,直接描述了视速率U与本征速度U。—随着视分量角α的变化而变化,观测中,视分量角一直在渐渐变大,由0向π/2变化,渐变为于π。
对于年自行值为1角秒的天体,过地球天顶,有四年视速率为0,对于年自行值为0.5角秒的天体,过地球天顶,有八年视速率为0。
巴纳德星的过去与未来,见表1;
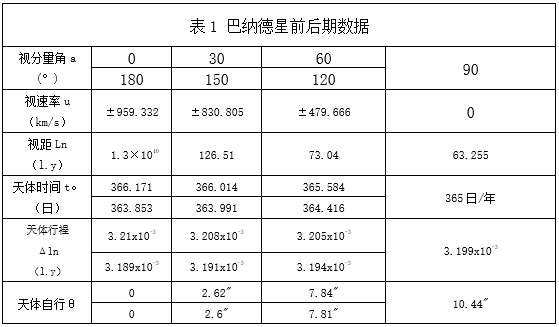
由表1的数据可得,巴纳德星相对太阳系,作匀速直线运动(没有外力作用下),初始(视分角为0)视速率为本征速度,渐运动至地球天顶时(P。),视速率由本征速度,渐变为0,再运动至末了(分量角为180),视速率由0渐变为本征速度。
地球时间一年为365日(取整数),而巴纳德星相对地球,由初始为366.171日,运动至地球天顶时,为365日,与地球年日相同,再运动至末了,巴纳德星年日继续变短,变为363.853日,巴纳德星相对了地球,从初始至末了,巴纳德星年日的变化,由366.171日至365日至363.853日。
是巴纳德星年日发生了变化了吗,见图3-3

一光源沿x轴以0.5光速运动,至x1处的瞬间,发射光讯号①,过一秒至x2处发射光讯号②,此瞬间①讯号刭达x。处,观测者计录时间,经过0.5秒,观测者计录下②光讯号,测得①②光讯号观测时间间隔为0.5秒,而光源发射①②光讯号的时间间隔为一秒。
光源确确实实以间隔一秒发射了①②光讯号,而测者确确实实以0.5秒间隔接收了①②光讯号,这是因为光讯号①与②以不同的光程到达测者。
光源运动到x3处发射③光讯号,经过一秒到达x4处发射④光讯号,此瞬间③讯号到达x。测者,测者开始计时,此瞬间而光源正到达x4,处,发射④光讯号,光讯号④经过1.5秒到达x。,测者计录下③④讯号的时间间隔为1.5秒。
光源以相同的一秒时间间隔发射了①②与③④光讯号,测者却以0.5秒与1.5秒间隔接收了①②与③④光讯号,是因为①②与③④讯号以不同的光程到达测者,而发生了时间效应!
[2] 式为时间效应式,地球年日是不变的量,得到天体巴纳德星的年日是个变量!
将[2]式天体时t。2(t。)设为不变的量,地球时t′(t)成了变量,
[2]式如下;
t = t。(1-cosaU。/C。) [9]
如图3-2,光源运动速度U。=0.5C。,发射脉冲光讯号①̖②̖③…周期t。=1秒,初始向着测者运动,视分量角a=0,测者测下周期t=0.5秒,光源相对测者运动,形式如图1,测者测下光源脉冲周期如表2;
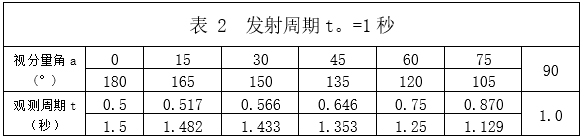
由表2知道,观测周期在渐渐变慢。
由[8]式得到表1天体自行θ项;视分量角a为0度与180度时,年自行值为0度,当巴纳德星运动至地球天顶(P。)时,视速率为0,年自行值为最大10.44″。
2022年视分童角a=83°40′16.2″,视距L=63.642光年,巴纳德星时t。=365.128日,自行程Δl n=0.00320光年,将以上数据代入[8]式,得年自行值θ=10.31″。
由表1知道,巴纳德星运动至地球天顶,年自行值为最大(10.44")天顶距为63.255光年,如在更远的天顶距上,其年自行值如何,见表3;
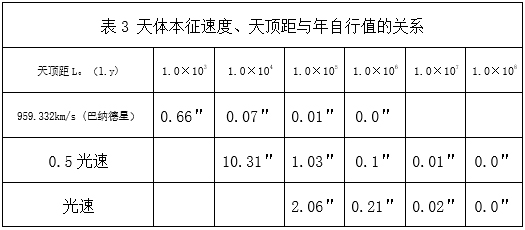
由表3知,巴纳德星天顶距一千光年时,其年自行值为0.66",十万光年时,其年自行值为0.01"了。
就是达到光速的天体,其地球天顶距为一千万光年,其年自行值也只是0.02"了,到一亿光年,其年自行值为0了,无法测出其自行了。
验证㈠;巴纳德星至地球天顶(P。还要2千多年,界时视速率为0,年自行值最大
(10.44″),一年一年的观测,视速率一年比一年小,年自行值一年比一年大。
验证㈡;由表1知天体运动至地球天顶(P。),其视速率为0,其年自行值为最大。一天体,视速率U1=20km/s,年自值为1.0″,过了4年,自行了θ=4.0″,视速率U2=19.8km/s,兰移天体,将以上数据代入[1]式,得视分量角a=89°53′20″,该天体的本征速度U。
U。=10313.259km/s,
4年自行程Δl n=0.137605光年。
将θ、a、Δl n代入[3]式;
得:视距L=7095.770光年。
如果第一年观测的视速率U1=19.8km/s,笫4年观测的祝速率U2=20km/s,红移天体,4年自行仍为
θ=4.0″,将以上数据代入[1]式
得视分量角a= -89°53′24″
得本征速度U。=10313.259km/s
得4年行程Δl n=0.137605光年
将θ、a、Δl n代入[3]式;
得:视距L= -7095.772光年。
将天体年自行值0.5″,4年自行θ=2.0″U1=20km/s U2=19.8km/s 代入[1]式
得视分量角a=89°56′40″
得本征速度U。=20626.490km/s
得4年行程Δl n=0.27521光年
将θ、a、Δl n代入[3]式;
得:视距L=28383.082光年。
验证㈢:所有存在自行的天体,兰移的,其视速率都在变慢,红移的,其视速率都在变快【4】,往后天文上的观测会得到验证。
- 梁世铎,时频效应实验及数学关系式的验证[J],浙江交通职业学院学报,2018,(3):47-50
- 梁世铎,时间效应[J],温州师范学院学报,自然科学版,1995年第6期,51-55
- (美)L.阿西摩夫.宇宙[M].北京:科学出版社,1984:35-37.
- 2016年中国天文年历,中国科学院紫金山天文台编[G],北京,科学出版社,202-445